Advanced: Control your flow

Here we dive a bit deeper in advanced flow control in Noodles. Starting with a recap into for-loops, moving on to conditional evaluation of workflows and standard algorithms. This chapter will also go a bit deeper into the teritory of functional programming. Specifically, we will see how to program sequential loops using only functions and recursion.

If you are new to the concepts of recursion, here is some nice material to start with:

Recap: for loops

In the Translating Poetry tutorial we saw how we could create parallel for loops in Noodles. To recap, let’s reverse the words in a sentence. Assume you have the following for-loop in Python:

sentence = 'the quick brown fox jumps over the lazy dog'
reverse = []

def reverse_word(word):
    return word[::-1]

for word in sentence.split():
    reverse.append(reverse_word(word))

result = ' '.join(reverse)
print(result)

eht kciuq nworb xof spmuj revo eht yzal god

There is a pattern to this code that is better written as:

reverse = [reverse_word(word) for word in sentence.split()]
result = ' '.join(reverse)
print(result)

eht kciuq nworb xof spmuj revo eht yzal god

This last version can be translated to Noodles. Assume for some reason we want to schedule the reverse_word function (it takes forever to run on a single core!). Because reverse_words becomes a promise, the line with ' '.join(reverse) also has to be captured in a scheduled function.

import noodles

@noodles.schedule
def reverse_word(word):
    return word[::-1]

@noodles.schedule
def make_sentence(words):
    return ' '.join(words)

reverse_words = noodles.gather_all(
    reverse_word(word) for word in sentence.split())
workflow = make_sentence(reverse_words)

from noodles.tutorial import display_workflows
noodles.tutorial.display_workflows(prefix='control', quick_brown_fox=workflow)

quick-brown-fox

This example shows how we can do loops in parallel. There are cases where we will need to do loops in a serialised manner. For example, if we are handling a very large data set and all of the computation does not fit in memory when done in parallel.

There are hybrid divide and conquer approaches that can be implemented in Noodles. We then chunk all the work in blocks that can be executed in parallel, and stop when the first chunk gives us reason to. Divide-and-conquer can be implemented using a combination of the two looping strategies (parallel and sequential).

Sequential loops are made using recursion techniques.

Recursion

Sequential loops can be made in Noodles using recursion. Comes the obligatory factorial function example:

from noodles.tutorial import display_text

def factorial(x):
    if x == 0:
        return 1
    else:
        return factorial(x - 1) * x

display_text('100! = {}'.format(factorial(100)))

100! = 933262154439441526816992388562667004907159682643816214685929638 … 0000000

There is a problem with such a recursive algorithm when numbers get too high.

try:
    display_text('10000! =', factorial(10000))
except RecursionError as e:
    display_text(e)

maximum recursion depth exceeded in comparison

Yikes! Let’s head on. And translate the program to Noodles. Suppose we make factorial a scheduled function, we cannot multiply a promise with a number just like that (at least not in the current version of Noodles). We change the function slightly with a second argument that keeps count. This also makes the factorial function tail-recursive.

@noodles.schedule
def factorial(x, acc=1):
    if x == 0:
        return acc
    else:
        return factorial(x - 1, acc * x)

result = noodles.run_single(factorial(10000))

display_text('10000! = {}'.format(result))

10000! = 2846259680917054518906413212119868890148051401702799230794179 … 0000000

Yeah! Noodles runs the tail-recursive function iteratively! This is actually very important. We’ll do a little experiment. Start your system monitor (plotting a graph of your memory usage) and run the following snippets. We let every function call to factorial gobble up some memory and to be able to measure the effect of that we insert a small sleep. Fair warning: With the current setting of gobble_size and running 50 loops, the first version will take about 4GB of memory. Just change the size so that a measurable fraction of your RAM is taken up by the process and you can see the result.

import numpy
import time
from copy import copy

gobble_size = 10000000

@noodles.schedule(call_by_ref=['gobble'])
def mul(x, y, gobble):
    return x*y

@noodles.schedule(call_by_ref=['gobble'])
def factorial(x, gobble):
    time.sleep(0.1)
    if x == 0:
        return 1
    else:
        return mul(factorial(x - 1, copy(gobble)), x, gobble)

gobble = numpy.zeros(gobble_size)
result = noodles.run_single(factorial(50, gobble))

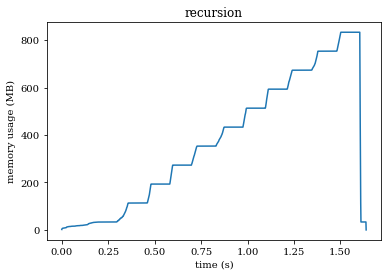
We passed the gobble argument by reference. This prevents Noodles from copying the array when creating the workflow. If you have functions that take large arrays as input and you don’t change the value of the array in between calls this is a sensible thing to do. On my machine, running only 10 loops, this gives the following result:

Try to understand why this happens. We have reserved a NumPy array with gobble_size (\(10^7\)) floating points of 8 bytes each. The total size in bytes of this array is \(8 \times 10^7\ MB\). In each recursive call to factorial the array is copied, so in total this will use \(10 \cdot 8 \times 10^7\ MB = 800\ MB\) of memory!

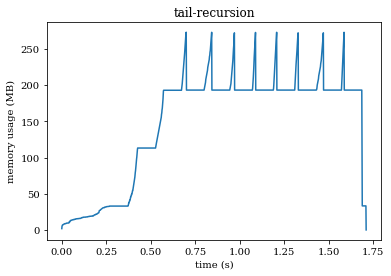
The next version is tail-recursive. This should barely make a dent in your memory usage!

@noodles.schedule(call_by_ref=['gobble'])
def factorial_tr(x, acc=1, gobble=None):
    time.sleep(0.1)
    if x == 0:
        return acc
    else:
        return factorial_tr(x - 1, mul(acc, x, gobble), copy(gobble))

gobble = numpy.zeros(gobble_size)
result = noodles.run_single(factorial_tr(50, gobble=gobble))

Now, the factorial function is still recursive. However, since returning a call to the factorial function is last thing we do, the intermediate results can be safely thrown away. We’ll have in memory the original reference to gobble and one version in the Noodles run-time for the last time factorial returned a workflow where gobble.copy() was one of the arguments. In total this gives a memory consumption of \(160\ MB\) (plus a little extra for the Python run-time itself). We see peeks that reach over \(250\ MB\) in the graph: this is where gobble is being copied, after which the garbage collector deletes the old array.

Try to understand why this happens. In the first case the function returns a new workflow to be evaluated. This workflow has two nodes:

display_workflows(
    prefix='control',
    factorial_one=noodles.unwrap(factorial)(10, '<memory gobble>'))

factorial-one

To evaluate this workflow, Noodles first runs the top node factorial(9, '<memory gobble>'). When the answer for this function is obtained it is inserted into the slot for mul(-, 10). Until the entire workflow is evaluated, the <memory gobble> remains in memory. Before this happens the factorial function is called which copies the gobble and creates a new workflow! We can write this out by expanding our algorithm symbolically \(f(x) = x \cdot f(x-1)\):

\[\begin{split}\begin{align} f(10) &= 10 \cdot f(9)\\ &= 10 \cdot (9 \cdot f(8))\\ &= 10 \cdot (9 \cdot (8 \cdot f(7)))\\ &\dots\\ &= 10 \cdot (9 \cdot (8 \cdot (7 \cdot (6 \cdot (5 \cdot (4 \cdot (3 \cdot (2 \cdot 1))))))))\\ &= 10 \cdot (9 \cdot (8 \cdot (7 \cdot (6 \cdot (5 \cdot (4 \cdot (3 \cdot 2)))))))\\ &= 10 \cdot (9 \cdot (8 \cdot (7 \cdot (6 \cdot (5 \cdot (4 \cdot 6))))))\\ &\dots \end{align}\end{split}\]

Now for the tail-recursive version, the workflow looks a bit different:

display_workflows(
    prefix='control',
    tail_recursive_factorial=noodles.unwrap(factorial_tr)(10, gobble='<memory gobble>'))

tail-recursive-factorial

First the mul(1, 10, '<memory gobble>') is evaluated. Its result is inserted into the empty slot in the call to factorial_tr. This call returns a new workflow with a new copy of <memory gobble>. This time however, the old workflow can be safely deleted. Again, it helps to look at the algorithm symbolically, given \(f(x, a) = f(x-1, x \cdot a)\):

\[\begin{split}\begin{align} f(10, 1) &= f(9, (10 \cdot 1))\\ &= f(9, 10)\\ &= f(8, (9 \cdot 10))\\ &= f(8, 90)\\ &= f(7, (8 \cdot 90))\\ &\dots \end{align}\end{split}\]

Conditional evaluation

But Python has more statements for flow control! The conditional execution of code is regulated through the if statement. You may want to make the exection of parts of your workflow conditional based on intermediate results. One such instance may look like this:

@noodles.schedule
def method_one(x):
    pass

@noodles.schedule
def method_two(x):
    pass

@noodles.schedule
def what_to_do(x):
    if condition(x):
        return method_one(x)
    else:
        return method_two(x)

We’ve put the if-statement inside the scheduled function what_to_do. This returns a new workflow depending on the value of x. We can no longer get a nice single graph picture of the workflow, because the workflow doesn’t exist! (there is no spoon …) We can work through a small example from the Python tutorial: computing prime numbers.

for n in range(2, 10):
    for x in range(2, n):
        if n % x == 0:
            print(n, 'equals', x, '*', n//x)
            break
    else:
        # loop fell through without finding a factor
        print(n, 'is a prime number')

2 is a prime number
3 is a prime number
4 equals 2 * 2
5 is a prime number
6 equals 2 * 3
7 is a prime number
8 equals 2 * 4
9 equals 3 * 3

The core computation in this example is the n % x == 0 bit. So we start by creating a scheduled function that does that.

@noodles.schedule
def divides(n, x):
    return n % x == 0

Noodles can parallelize the inner loop, but this gives a problem: how do we know when to stop? There is no way to get it both ways.

First, we’ll see how to do the parallel solution. We’ll compute the divides(n, x) function for the values of n and x and then filter out those where divides gave False. This last step is done using the compress function.

@noodles.schedule
def compress(lst):
    """Takes a list of pairs, returns a list of
    first elements of those pairs for which the
    second element is thruthy."""
    return [a for a, b in lst if b]

Using the compress function we can write the Noodlified parallel version of the filter function. We’ll call it p_filter for parallel filter.

?filter

Init signature: filter(self, /, *args, **kwargs)
Docstring:
filter(function or None, iterable) --> filter object

Return an iterator yielding those items of iterable for which function(item)
is true. If function is None, return the items that are true.
Type:           type
Subclasses:

Using the generic p_filter function we then write the function find_factors that finds all integer factors of a number in parallel. Both p_filter and find_factors won’t be scheduled functions. Rather, together they build the workflow that solves our problem.

def p_filter(f, lst):
    return compress(noodles.gather_all(
        noodles.gather(x, f(x)) for x in lst))

def find_factors(n):
    return p_filter(lambda x: divides(n, x), range(2, n))

display_workflows(prefix='control', factors=find_factors(5))

factors

No we can run this workflow for all the numbers we like.

result = noodles.run_parallel(
    noodles.gather_all(noodles.gather(n, find_factors(n))
                       for n in range(2, 10)),
    n_threads=4)

for n, factors in result:
    if factors:
        print(n, 'equals', ', '.join(
            '{}*{}'.format(x, n//x) for x in factors))
    else:
        print(n, 'is prime')

2 is prime
3 is prime
4 equals 2*2
5 is prime
6 equals 2*3, 3*2
7 is prime
8 equals 2*4, 4*2
9 equals 3*3

Few! We managed, but if all we wanted to do is find primes, we did way too much work; we also found all factors of the numbers. We had to write some boiler plate code. Argh, this tutorial was supposed to be on flow control! We move on to the sequential version. Wait, I hear you think, we were using Noodles to do things in parallel!?? Why make an effort to do sequential work? Well, we’ll need it to implement the divide-and-conquer strategy, among other things. Noodles is not only a framework for parallel programming, but it also works concurrent. In the context of a larger workflow we may still want to make decision steps on a sequential basis, while another component of the workflow is happily churning out numbers.

Find-first

Previously we saw the definition of a Noodlified filter function. How can we write a find_first that stops after finding a first match? If we look at the workflow that p_filter produces, we see that all predicates are already present in the workflow and will be computed concurrently. We now write a sequential version. We may achieve sequential looping through recursion like this:

def find_first(f, lst):
    if not lst:
        return None
    elif f(lst[0]):
        return lst[0]
    else:
        return find_first(f, lst[1:])

However, if f is a scheduled function f(lst[0]) will give a promise, and this routine will fail.

@noodles.schedule
def find_first_helper(f, lst, first):
    if first:
        return lst[0]
    elif len(lst) == 1:
        return None
    else:
        return find_first_helper(f, lst[1:], f(lst[1]))

def find_first(f, lst):
    return find_first_helper(f, lst, f(lst[0]))

noodles.run_single(find_first(lambda x: divides(77, x), range(2, 63)))

7

That works. Now suppose the input list is somewhat harder to compute; every element is the result of a workflow.

Appendix: creating memory profile plots

%%writefile test-tail-recursion.py
import numpy
import noodles
import time
from copy import copy

@noodles.schedule(call_by_ref=['gobble'])
def factorial_tr(x, acc=1, gobble=None):
    time.sleep(0.1)
    if x == 0:
        return acc
    else:
        return factorial_tr(x - 1, acc * x, copy(gobble))

gobble_size = 10000000
gobble = numpy.zeros(gobble_size)
result = noodles.run_single(factorial_tr(10, gobble=gobble))

Writing test-tail-recursion.py

%%writefile test-recursion.py
import numpy
import noodles
import time
from copy import copy

@noodles.schedule(call_by_ref=['gobble'])
def mul(x, y, gobble):
    return x*y

@noodles.schedule(call_by_ref=['gobble'])
def factorial(x, gobble):
    time.sleep(0.1)
    if numpy.all(x == 0):
        return numpy.ones_like(x)
    else:
        return mul(factorial(x - 1, copy(gobble)), x, gobble)

gobble_size = 10000000
gobble = numpy.zeros(gobble_size)
result = noodles.run_single(factorial(10, gobble))

Writing test-recursion.py

!pip install matplotlib
!pip install memory_profiler

Requirement already satisfied: matplotlib in /home/johannes/.local/share/workon/marin/lib/python3.7/site-packages (3.1.1)
Requirement already satisfied: python-dateutil>=2.1 in /home/johannes/.local/share/workon/marin/lib/python3.7/site-packages (from matplotlib) (2.8.0)
Requirement already satisfied: kiwisolver>=1.0.1 in /home/johannes/.local/share/workon/marin/lib/python3.7/site-packages (from matplotlib) (1.1.0)
Requirement already satisfied: pyparsing!=2.0.4,!=2.1.2,!=2.1.6,>=2.0.1 in /home/johannes/.local/share/workon/marin/lib/python3.7/site-packages (from matplotlib) (2.4.2)
Requirement already satisfied: numpy>=1.11 in /home/johannes/.local/share/workon/marin/lib/python3.7/site-packages (from matplotlib) (1.17.3)
Requirement already satisfied: cycler>=0.10 in /home/johannes/.local/share/workon/marin/lib/python3.7/site-packages (from matplotlib) (0.10.0)
Requirement already satisfied: six>=1.5 in /home/johannes/.local/share/workon/marin/lib/python3.7/site-packages (from python-dateutil>=2.1->matplotlib) (1.12.0)
Requirement already satisfied: setuptools in /home/johannes/.local/share/workon/marin/lib/python3.7/site-packages (from kiwisolver>=1.0.1->matplotlib) (41.4.0)
Collecting memory_profiler
  Downloading https://files.pythonhosted.org/packages/9f/fe/1fca7273dd111108f204a686b12a12b6422d405fe4614087aa7d5a66ea87/memory_profiler-0.55.0.tar.gz (40kB)
     |████████████████████████████████| 40kB 2.9MB/s eta 0:00:01
Requirement already satisfied: psutil in /home/johannes/.local/share/workon/marin/lib/python3.7/site-packages (from memory_profiler) (5.6.3)
Building wheels for collected packages: memory-profiler
  Building wheel for memory-profiler (setup.py) ... done
  Created wheel for memory-profiler: filename=memory_profiler-0.55.0-cp37-none-any.whl size=27173 sha256=1068b6f6ab5159d51df0e47f482548afff67d98feb0260a73155be3aad54408a
  Stored in directory: /home/johannes/.cache/pip/wheels/f0/ff/63/fdbff3f1e1b76ad4eae491dd5b190902906b093e93eb86dd5a
Successfully built memory-profiler
Installing collected packages: memory-profiler
Successfully installed memory-profiler-0.55.0

%%bash
rm mprofile_*.dat
mprof run -T 0.001 python ./test-tail-recursion.py
mprof run -T 0.001 python ./test-recursion.py

mprof: Sampling memory every 0.001s
mprof: Sampling memory every 0.001s

rm: kan 'mprofile_*.dat' niet verwijderen: No such file or directory

from pathlib import Path
from matplotlib import pyplot as plt
import numpy

plt.rcParams['font.family'] = 'serif'

def read_mprof(filename):
    lines = list(open(filename, 'r'))
    cmd = filter(lambda l: l[:3] == 'CMD', lines)
    mem = filter(lambda l: l[:3] == 'MEM', lines)
    data = numpy.array([list(map(float, l.split()[1:])) for l in mem])
    data[:,1] -= data[0,1]
    data[:,0] *= 1024**2
    return cmd, data

def plot_mprof(filename):
    cmd, data = read_mprof(filename)
    if 'tail' in next(cmd):
        figname = 'tail-recursion'
    else:
        figname = 'recursion'

    plt.plot(data[:,1], data[:,0] / 1e6)
    plt.xlabel('time (s)')
    plt.ylabel('memory usage (MB)')
    plt.title(figname)
    plt.savefig('control-' + figname + '-raw.svg', bbox_inches='tight')
    plt.show()

files = list(Path('.').glob('mprofile_*.dat'))
for f in files:
    plot_mprof(f)
    plt.close()